How to Identify Musical Intervals (Music Theory)

How to Identify Musical Intervals (Music Theory)

Video transcripts below may be slightly inaccurate due to software

0:00
intervals,

0:00
or how we measure musical distance between notes,

0:03
being able to identify labeled them obsessing concretely about music. By making distinct categories in our brain. For all the different sounds, improve our perception and understanding of music, we can measure up melodies. Precisely. Improving intonation, and intervals are the building blocks of how we create courts harmonize, composing, counterpoint, and host of other crucial musical skills. The first step and mastering intervals, is being able to label them. And that’s what I’m going to teach you. Now, in western music. The smallest division of musical distance is to semi tone of a half step, which is the distance between any two adjacent notes on a piano, we call this interval, the minor second. And

0:50
in a sense, you can think of all other interval distances, as some number of semi tones added together, the next white, this musical distance is to semi tones,

1:01
can we call it the major second

1:06
or third.

1:08
So you can memorize something like this chart, which would give you a pretty good chunk

1:15
to be really precise, we need a more systematic approach, because other reasons, there’s more than one name for each musical distance, and only context will tell you which lake is correct. And the interval naming system breaks down into two steps. The first is identifying the number of the interval, this is pure alphabetical distance, if you’re trying to figure out the interval between See, if you count from C to F, inclusively, C, D, E, F, is interval is a fourth,

1:52
how about from G sharp T, again, pure alphabet, so ignore the accidental G, A, B, C, D, E, that’s the sixth. Note that you always count the interval number from the lower to the upper note, you wouldn’t count from E, G, or from G down D,

2:15
because in both of those cases, you’d call this distance a third, which is incorrect. So you tried, what’s the interval number from f up to C sharp,

2:29
right, F, G, A, B, C, a fifth,

2:35
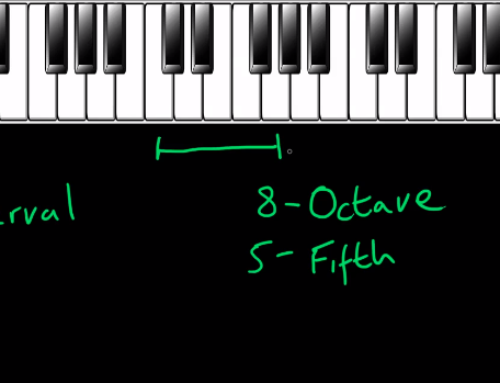
that’s important to know that we have a special name for to interval numbers, an interval number of one the same note C and C, or C to C sharp, we say is a unison in front interval number of eight, which again, would be like from C to C, or C and C sharp. But now with all the intervening notes between we call it an octave. Now at this point, it should be troubling you that the same interval number can apply to to obviously different musical distances, C to C, C to C sharp, both octaves. They’re not the same distance, and they couldn’t sound more different. So we need the next step to determine interval quality

3:18
to disambiguate them for interval quality. We handle

3:23
seconds thirds, sixth, and seventh one way and unison’s, fourth, fifth and octaves

3:29
another there are two different classes of interval, they sound different behave different, so we have a different naming scheme for each to account for that the unison’s fourth fifth and opt ins are pure extremely consonant sounding intervals. And so their default quality, if you will, is called perfect. That’s to say, for trying to identify interval and interval number happens to be a unison for us fifth one octave,

4:02
we use the test of whether the upper note of the interval is in the key of the lower note, if it is, we say, the interval is perfect. So let’s try about see to G to fifth. Now we test whether G is in the key of C. Well, the key of C has these notes, which contains G, the upper note is in the key of the lower note. So we say this is a perfect interval, a perfect fifth. And notice how pure and open this interval sounds

4:35
perfect indeed. And what if the upper note wasn’t in the key of the lower now what if we were trying to identify the interval of see to G flat? Well, the key of C doesn’t contain G flat, and G flat is a semi tone lower than what the QC does contain for that note letter G natural in such a case, we would call this a diminished interval, a diminished fifth, if we were looking at see to G sharp sharp as a semi tone higher than what the key contains. So we’d say it’s augmented, and that’s the rule set for this class of intervals. If the upper notes in the key of the lower we call perfect flat by a semi tone, we say it’s diminished sharp by a semi, we say it’s augmented,

5:29
you practice one, how about B flat, t natural?

5:34
First, we confirm the number B, C, D, E, it’s a fourth. So no, it belongs to this class interval. Now, we need to know the key of

5:47
B flat major contains these notes

5:51
is the upper note in the key of the lower

5:57
it isn’t B flat major contains he flats ease the semi tone higher than that. So we’d say this is an augmented fourth. Okay, for more practice on this class of interval, I’ve given you three more to try and identify have put the answer some of the description so you can check if done correctly. Now, let’s move on to the other class interval seconds, thirds, six, and seven. If the upper note of the interval is in the key of the lower know for these intervals, we say is major. Let’s try see to a sixth. Again, the QC has these notes. So A is in the key. So we say this is a major six.

6:46
Now what about seat a flat or the a flat is a semi tone lower than what we find in the QC Well, we’d say that’s a minor six see to a sharp me tone higher than what we find in the key is an augmented six similar procedure to the other class of intervals. But notice the default quality for these is major or is it’s perfect, but the other we have the same name for semi tone higher than what’s in the key of the lower say it’s augmented different names for a semi tone, lower major goes to minor perfect goes to diminished. Let’s try one together. How about D to F, it’s a third so belongs to this class of interval. And the key of D has these notes meaning it contains f sharps. So F natural doesn’t belong. It’s a semi tone lower than what’s in the key. So we say di to F, some minor third. Now here are three more intervals belonging to this class, try your hand identifying them and description. Now let’s identify interval without knowing in advance which class it belongs to us. We go will solidify the procedure for interval naming. Let’s do F to be first thing, we figure out the interval number at simply counting letters from the lower to the upper inclusively, so f

8:24
g a b, this is a fourth and knowing the interval number, we know which class of interval. This belongs to unison’s, fourth, fifth, and octaves have this naming scheme. And to apply this we need to know the key of the lower note of the interval in this case would be the key of F, F, G, A, B, flat, C, D, and E,

8:52
we ask ourselves is the upper note at the interval in this key, and it isn’t, the key f has be flats be natural system me tone higher than that, making this an augmented in an augmented fourth, let’s do one more G, F, sharp

9:12
first figure out the number, G, A, B, C, D, E, F, seventh mean belongs to the class of intervals of the second step six and sevens using this naming scheme, get the Q, the lower note G major, and we find the F sharp to top, notice the interval is in the key of the lower now. So this interval gets its default quality

9:37
of major G to F sharp is a major seventh. And that’s your procedure. First, you count alphabetically from the lower to the upper note of the interval inclusively, and this gives us the interval number, then we use the interval number to decide which of the two naming rules we apply if the interval number is a unison, fourth, fifth or octave, and the upper note of the interval is in the key of the lower note, we say the interval is perfect,

10:08
a semi tone higher it’s augmented, semi tone lower it’s diminished if the interval number is a second, third, sixth or seventh and the upper note of the interval is in the key of the lower know

10:21
we say the interval is major it’s a semi

10:23
higher than what’s in the key segmented semi to lower its minor

10:30
and that’s it that’s how you label intervals. Here are three more to try answer some the description and questions asking the comments. That’s all for now, so I don’t see you next time.

Music theory is often concerned with describing how musicians and composers make music, including tuning systems and methods of composition among other topics. Because of the ever-increasing perception of what constitutes music (see definition of music), the most comprehensive definition could be that music theory is a consideration of any sound phenomena, including silence, as it relates to music. These are not absolute guidelines; for example, the study of “music” in the curriculum of the College of Free Arts in Quadrivium, which was common in medieval Europe, was an abstract system of proportions carefully studied at a distance from actual musical practice.  However, this discipline in the Middle Ages became the basis of the discipline systems in later centuries and is generally included in modern studies on the history of music theory.

Music theory as a practical system includes the methods and concepts used by composers and other musicians to create music. The development, preservation and transfer of music theory can be found in the tradition of making oral and written music, musical instruments and other works of art. For example, the ancient instruments of Mesopotamia, China, and prehistoric sites around the world reveal details about the music they produced, and perhaps something of the musical theory that may have been used by their makers (see History of Music and Instruments Music). In ancient and living cultures around the world, the deep and long roots of music theory are clearly evident in oral instruments and traditions and in contemporary music making. Many cultures, at least as far back as ancient Mesopotamia and ancient China, also considered music theory in more formal ways such as written theses and music. Scientific and scientific traditions overlap, as many practical essays on music place themselves in the tradition of other treatises, which are cited regularly as scientific research refers to previous research.

In modern academia, music theory is a subfield of music science, a broader study of musical cultures and history. Fundamentalist, the theory of music is meditative work of music, of Greek εεωρία, viewing, viewing, contemplation, speculative, theoretical, also sight, scene.  As such, they are often concerned with abstract musical aspects such as tuning, tones, scales, consistency, dissonance, and rhythmic relationships, but there is also a set of theories concerning practical aspects such as the creation or performance of music, counterfeiting, E-mail. A person who studies, teaches or writes articles about music theory is a musical landscape. University studies, usually at the master’s or doctorate level, are required to teach as a track track in an American or Canadian university. Methods of analysis include mathematics, graphic analysis, and special analysis that can codify Western music. Comparative, descriptive, statistical and other methods are also used. Music theory books, especially in the United States of America, often contain elements of musical acoustics, musical codification considerations, tonal composition techniques (harmony and contrast), and other subjects.

Music Basics
Main article: aspects of music
Music consists of horizontal phenomena; “music theory” is considered how these phenomena are applied in music. The theory of music examines the melody, rhythm, symmetry, harmony, form, tonal systems, scales, synthesis, periods, consistency, dissonance, symmetrical ratios, audios, sound systems, composition, performance, synthesis, . .

Football stadium
Main article: Playground (music)

Center C (261.626 Hz) around this sound
The sound level is the degree of noise or the height of the tone, for example the difference between the middle C and the top C. The frequency of the sound waves that produce the pitch can be measured accurately, but the perception of the pitch is more complicated because individual observations from natural sources are usually a complex mix of many frequencies. Accordingly, theorists often describe the playground as a subjective sensation.

Frequencies are often assigned specific character names. Today most orchestras set the concert A (A above C medium on the piano) for a frequency of 440 Hz. This task is somewhat arbitrary; for example, in France in 1859, the same A was set to 435 Hz. These differences can have a noticeable effect on bell tools and other phenomena. Thus, in the historical performance of old music, tuning is often tuned to match the settings used in the period in which it was written. In addition, many cultures do not try to unify the pitch, often considering that they must be allowed to vary by genre, style, mood, etc.

The difference in color is called two interval intervals. The most basic interval is harmony, which is just two notes of the same pitch. An octave separator is two degrees, either a double or a half frequency. The unique characteristics of octaves have given rise to the concept of the pitch layer: the stadiums with the same name as the characters that occur in different octaves can be classified into one “layer” by ignoring the difference in the octave. For example, high C and low C are two members of the same grade class – the class containing each C.

Musical tuning systems or moods determine the exact size of time intervals. Control systems vary greatly within and between global cultures. In Western culture, there have long been many competing disciplines, all of which have different characteristics. At the international level, the system known as mood is the most widely used today because it is the most satisfying medium that allows fixed tuning tools (such as piano) to sound acceptable in all keys.

Tables and Conditions
Main articles: Music standard and musical style

Style of full and half steps in ionic mode or main range on C around this sound (Help · Info).
Notes can be arranged in a variety of metrics and styles. Western music theory generally divides the octave into a series of twelve tones called a chromatogram, in which the comma between the adjacent two tones is called a half or semi-silent step. Choose ringtones from this set of 12 and arrange them in styles of tones, tones and entire tones creates other ranges.

The most common measures are the seven tons, the minor harmonic, the minor minor, and the minor. Other examples of scales are the scale scale, the five-tone scale, or five tones, which is common in folk music and blues. Non-Western cultures often use scales that do not correspond to the division of twelve tones divided equally by octaves. For example, classical Ottoman, Persian, Hindi, and Arabic classical music systems often use repetitions of four-tone tones (half the size of half the word, as the name indicates), for example in “neutral” seconds (three degrees) or “two- They do not usually use the same quarter tone as a direct period.

In traditional Western notation, the metric used for configuration is usually referred to by a master signature initially to assign the tones that make up that metric. As the music advances, the playing fields may change and offer a different range. Music can be moved from one scale to another for different purposes, often to accommodate the singer’s range. This move increases or decreases the overall degree range, but maintains the relationships between the original scale. For example, switching from the C key to the D key increases all C C degrees evenly in a complete tone. Since the interpersonal relationships remain unchanged, the listener may not notice the transfer by the listener, but the other attributes may change significantly because the transformation changes the relationship between the total pitch range compared to the range of instruments or sounds that perform the music. This often affects the overall sound of music, as well as artistic effects on performers.